The Mathematics Behind Numbers - Making Sense of the World Around Us
Why This Post?
I loved mathematics. My three most favorite subjects in high school were Math, Physics, and Chemistry, especially Mathematics. I loved crunching those numbers and formulas, but sometimes we didn't truly understand them. I remember learning differential equations—I knew how to derive and integrate and understood that we needed integrals to calculate the area under a curve, which at the time was mind-blowing for me. The only way I understood how to calculate the volume of an irregular object back then was to immerse it in water and see how much it displaced. Area of irregular shape was uncharted territory before integrals. Similarly, when asked, "What is 1 divided by zero?" in lower grades, we were told it was undefined, likely to protect us from the truth—that it was infinity. If the teacher had explained that back then, they would also have had to explain infinity to kids who had just started multiplying; our small brains might have exploded!
All this is to say that in school, we mostly focused on using formulas and only a little on understanding what they mean and their applications. I wish I had invested more time to understand beyond numbers and the concepts more deeply!
So, here is a post for people who have brothers, sisters, children, or even students. We became better so that our next generation becomes exponentially better.
“There's a small group who can do the math. There's an even smaller group who can explain it. But those few who can do both, they become billionaires.”
The Mathematics Behind Numbers - Making Sense of the World Around Us
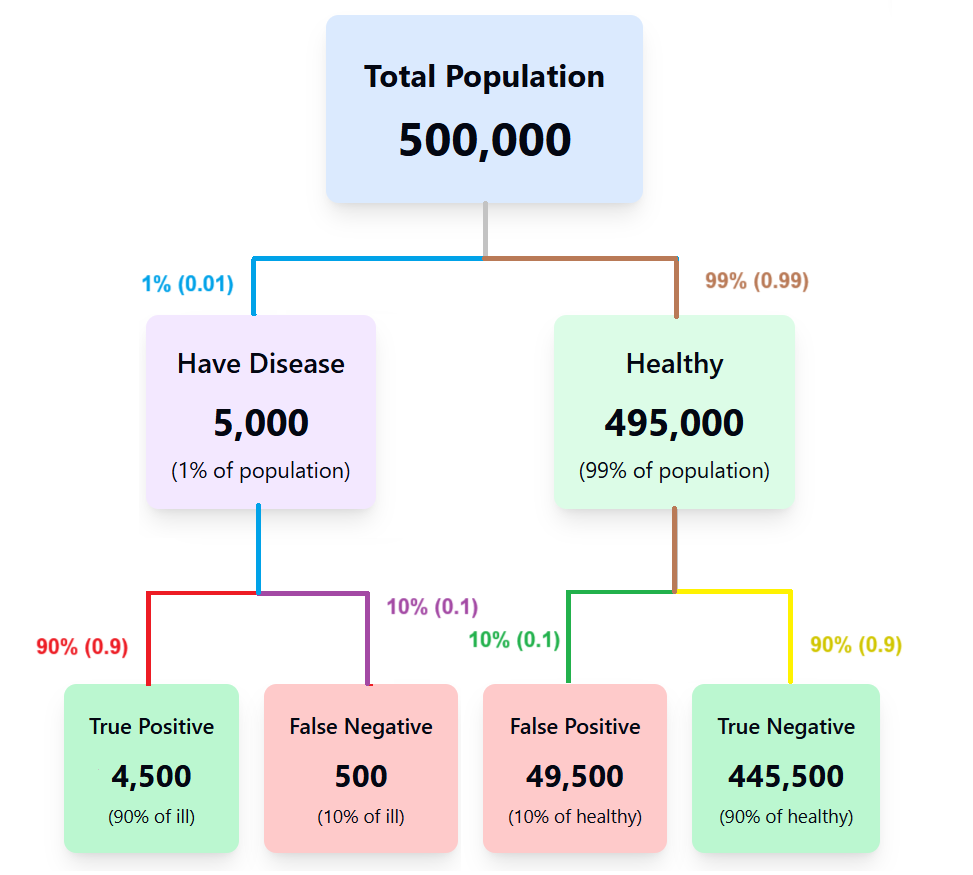
I recently stumbled upon an interesting question while reading a book, and it got me thinking about how we interpret medical tests. It goes like this
Suppose a disease that affects 1% of the population and you buy a quick test that claims to be 90% reliable to screen for a rare immune deficiency, and you test positive. Should you be worried? Does that mean you have 90% chance, you are positive? Just how likely is it that you actually have the disease?
"You'd think that a 90% accurate test means you're almost certainly sick, but that isn't quite right."
The answer isn't as straightforward as it seems, but it will tell us much more if we understand the mathematics behind it after all mathematics is a model (super clear glasses to see the world better than our intuition) and our intuition are mostly wrong, and it comes down to something called Bayes' Theorem. Let's take a look at the numbers and what they mean for you and your health.
The Scenario
A disease that affects 1% of the population.
To make it concrete, let’s say there are 500,000 people, and 5,000 (1%) of them have this disease. You find out that a rapid test for this disease has 90% accuracy. But—here's the catch—even the most reliable tests have limitations. This test misses 10% of true cases, or worse, 10% of healthy people are mistakenly told, they are positive (have the disease - you might end up here because of the 10% error rate).
Now, you took the test, and it comes back positive. A sinking feeling sets in: Does this mean you almost certainly have it? You'd think that a 90% accurate test means you're almost certainly sick, but that isn't quite right.
Understanding Probabilities
Here's the subtle truth that Bayes' Theorem helps uncover: Because the disease is so rare, even a highly accurate test can give a lot of false positives (mis diagnosed as you have it even though you do not). So, what does a positive result actually mean for you?
Let’s break this down step by step
Out of 500,000 people, only 5,000 have the disease.
Since the test is 90% accurate, it correctly identifies 4,500 sick individuals. But it also misses 500 of them (false negatives).
On the flip side, of the 495,000 healthy people, the test mistakenly identifies 49,500 as positive (false positives).
When you look at those numbers, you realize that out of everyone who tests positive, most people are actually false positives (Misdiagnosed). In fact, using Bayes' Theorem, the chance that you actually have the disease given that you tested positive turns out to be only about 8.33%. in other words, the chance that you're healthy despite a positive test (the test shows you have the disease)? A surprising 91.67%.
Perspective on Test Results
This is huge, there could be almost 92% chance you are healthy.We tend to put a lot of trust in numbers, especially when they involve our health. But sometimes, numbers can be misleading if we don't consider the bigger picture—like how rare a condition is in the first place.
The key insight here is not that you have a very low chance of having the disease, but rather that the majority of the population—495,000 out of 500,000—is not affected by the disease. Due to the 10% error rate of the test, that means if 495,000 (99%) of people were to take the test the 10% (49,500) people would be potentially mis-diagnosed (False Positive) which is still very large compared to the 1% misdiagnosis (False Negative). This leads to a large number of false positives among healthy individuals. This effect is amplified when dealing with a rare disease, making it far more likely that a positive result is actually incorrect. This says a lot about percentage perception: even a small error rate can lead to a big problem when most people are healthy, giving you the most probability of being misdiagnosed (a false positive). On the flip side, it gives a much lower probability that you are actually sick given that you test positive—just 8.3%.
So, What If the test apparatus accuracy increased to 95% (Or Error Rate reduced by 5%)?
Now, let's take it one step further and ask - What if the error rate of the test was reduced to 5% instead of 10%? How would that affect the results?
Total Population: 500,000 people.
People with the Disease: 5,000 people (1%).
True Positives: If the test correctly identifies 95% of the people with the disease, then 4,750 people are correctly identified as having the disease.
False Negatives: The test misses 5% of the people who actually have the disease, which means 250 people are incorrectly told they do not have the disease.
People without the Disease: 495,000 people (99%).
False Positives: If the test incorrectly identifies 5% of the healthy people as positive, then 24,750 healthy people are incorrectly told they have the disease.
True Negatives: 95% of the healthy individuals are correctly identified as not having the disease, which means 470,250 people are correctly told they are healthy.
Calculating the Probability of Actually Being Sick Given a Positive Test
To calculate the updated probability that you are actually sick given a positive test result, we use Bayes' Theorem:
True Positives: 4,750 people.
False Positives: 24,750 people.
Total Positives: 4,750 (true positives) + 24,750 (false positives) = 29,500 people.
The probability that you are actually sick given that you tested positive is:
What Does This Mean?
By reducing the error rate of the test from 10% to 5%, the probability that you actually have the disease given a positive test result doubled, from 8.3% to 16.1%. in other words, there could be 83.9% Chance you could be healthy. still huge!
While this is a significant improvement, it still means that the majority of people who test positive are false positives. This highlights just how challenging it can be to accurately diagnose rare conditions, even with a relatively reliable test.
What If the Test Reliability Increased to 99%?
Now, let’s take it a step further and increase the test reliability to 99%. How does that change the results?
Total Population: 500,000 people.
People with the Disease: 5,000 people (1%).
True Positives: If the test correctly identifies 99% of the people with the disease, then 4,950 out of 5,000 people are correctly identified as having the disease.
False Negatives: The test misses 1% of the people who actually have the disease, which means 50 people are incorrectly told they do not have the disease.
People without the Disease: 495,000 people (99%).
False Positives: If the test incorrectly identifies 1% of the healthy people as positive, then 4,950 healthy people are incorrectly told they have the disease.
True Negatives: 99% of the healthy individuals are correctly identified as not having the disease, which means 490,050 people are correctly told they are healthy.
Updated Probability Calculation
To calculate the updated probability that you are actually sick given a positive test result:
True Positives: 4,950 people.
False Positives: 4,950 people.
Total Positives: 4,950 (true positives) + 4,950 (false positives) = 9,900 people.
The probability that you are actually sick given that you tested positive is:
What Does This Mean?
With the test reliability increased to 99%, the probability that you actually have the disease given a positive test result becomes 50%. This means that even with a highly accurate test, if you test positive, you still have only a 50-50 chance of actually being sick.
This highlights how challenging it is to diagnose rare diseases accurately, even with highly reliable tests. The rarity of the condition and the proportion of false positives still play significant roles in determining the actual likelihood of being sick.
A Subtle Lesson in Probability
So next time you hear about a medical test result, ask yourself: What's the prevalence of the condition in the population? Is a positive result really what it seems? This is one of those cases where a simple question led me to rethink how we perceive medical information and probabilities.
The lesson I learned? Numbers are powerful, but the context is everything.
